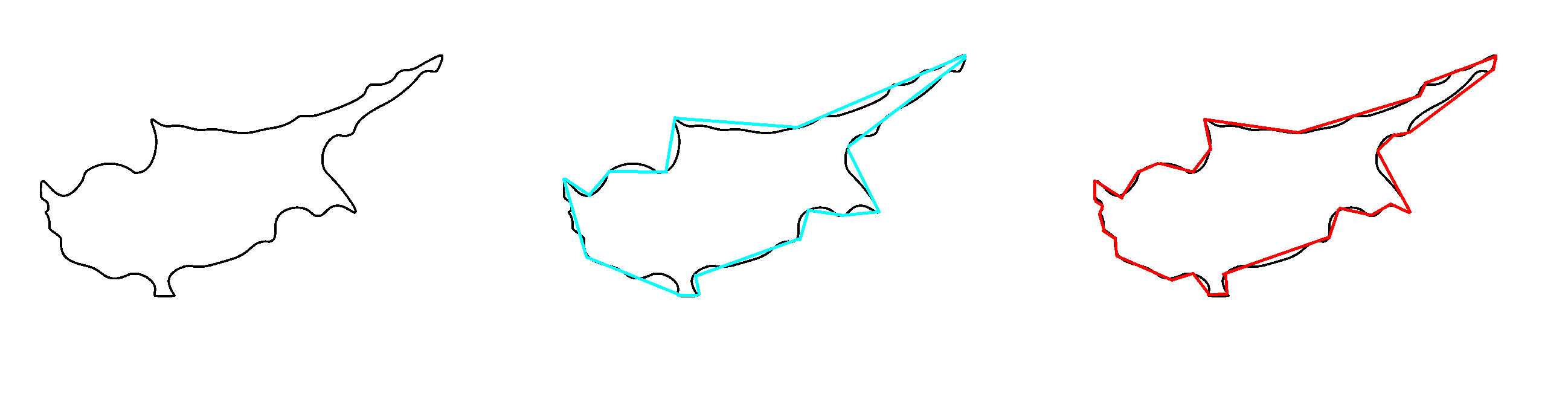
Kıbrıs’ın kıyı şeridi ne kadardır? Bu soru göründüğünden çok daha karmaşıktır ve yanıtı bizleri derin ve güzel bir matematiğe: Fraktallar teorisine götürür
Kıyı şeridinin uzunluğunu ölçmek kolay bir iş değildir. Düz çizgilerin uzunluğunun ölçülmesi kolaydır; eğrilerin ise kolay değildir. Herhangi bir eğrinin uzunluğu düz çizgilerle yaklaşık olarak hesaplanabilir ve Şekil 1, Kıbrıs'ın kıyı şeridi için bunu yapmanın iki yolunu göstermektedir: ilk yol camgöbeği renginde 16 düz doğru parçasıyla, ikincisi ise kırmızı renkte 32 düz doğru parçasıyladır. İki nokta arasındaki en kısa mesafe düz bir çizgi olduğundan, daha fazla doru parçası kullanmak toplam uzunluğu artıracaktır; dolayısıyla kırmızı doğru parçalarının toplam uzunluğu, camgöbeği doğru parçalarının toplam uzunluğundan daha uzun olur. İkinci şekil ilkinden daha etkili görünüyor çünkü kırmızı yol gerçek sahil şeridine camgöbeği olandan daha yakın bir yaklaşımdır. Bununla birlikte, kırmızı yol hala kesin değildir: Kıyı şeridinin her burun, körfez ve girişini ölçen yüzlerce veya binlerce doğru parçalarıyla yaklaşımlar çizmek mümkündür. Peki nerede duracağız? Yaklaşımı daha derin bir seviyeye taşımak, her kumsaldaki her kaya ve çakıl taşının etrafını ölçmek mümkündür ve bu, uzunluğu daha da arttıracaktır. Yaklaşım iyileştikçe uzunluk da uzuyor gibi görünüyor. Peki Kıbrıs'ın gerçek kıyı şeridi uzunluğu nedir?
Aslında bu sorunun net bir cevabı yok. Çember gibi ideal bir matematiksel eğri için, bir limit işlemi kullanarak düz olmasa bile uzunluğu için kesin bir değer elde etmek mümkündür: düz çizgilerle git gide daha yakın yaklaşımlar, eğrinin uzunluğu için git gide daha büyük değerler verecektir, fakat bu daha büyük değerler hiçbir zaman gerçek uzunluk olan sabit bir değerin ötesine geçmeyecektir. Kıbrıs'ın kıyı şeridi gibi bir eğri için her ölçekte kıpırdanma vardır: yarımadalar ve körfezlerin etrafında büyük olanlar, burunlar ve nehir ağızlarının etrafında küçük olanlar, kayalar ve erozyonun etrafında ufak tefek olanlar,... kıpırdanmaları ölçmeyi durduracak bariz bir ölçek yoktur ve dolayısıyla gerçek kıyı şeridinin kesin bir değeri yoktur.
“Her ölçekte yapıya" sahip olan matematiksel bir şekle fraktal denir. Kıyı şeridi problemi gerçek hayattaki bir fraktal örneğidir, çünkü kıyı şeridinde her ölçekte kıpırdanma vardır. Matematiksel örnekler arasında Şekil 2'deki Sierpinski üçgeni ve Şekil 3'teki Koch kar tanesi yer alır; bu resimlerin her ikisi de tam olarak çizilemeyen ideal matematiksel nesnelere yalnızca yaklaşık değerlerdir.
Fraktalların tam sayı olmayan boyutları da vardır. Bunu anlamanın kolay bir yolu, aynı şeklin daha büyük başka bir kopyasını oluşturmak için aynı şeklin kaç kopyasına ihtiyaç duyulduğunu düşünmektir. Bir kare iki boyutludur ve iki katı büyüklükte yeni bir kare oluşturmak için dört (iki üssü ikiye eşit) kareye ihtiyaç vardır. Bir küp üç boyutludur ve iki katı büyüklükte yeni bir küp oluşturmak için sekiz (iki üssü üçe eşit) küp gerekir. Sierpinski üçgeni için, iki katı boyutta yeni bir kopya oluşturmak için üç kopyaya ihtiyaç vardır, dolayısıyla boyut, üçün iki üssü D'ye eşit olacak şekilde bir D sayısıdır. Böyle bir tam sayı D yoktur, dolayısıyla boyutu Sierpinski üçgeni tam sayı olmamalıdır!
En sıra dışı fraktal şekillerden biri, Şekil 4'te gösterilen Mandelbrot kümesidir. Karmaşık sayıları içeren basit bir matematiksel formülle tanımlanır ve şaşırtıcı bir yapı derinliği sergiler: insanlar Mandelbrot kümesinin büyütüldüğü saatler süren çevrimiçi videolar hazırlamışlardır ve her ölçekte yeni güzel desenler ve şekiller ortaya çıkmaktadır. Tüm bu şekiller tek bir basit matematik formülünden ortaya çıkıyor: Bunları kimse tasarlamadı, yalnızca hesapladı. Mandelbrot kümesinin pek çok özelliği matematikçiler tarafından hâlâ bilinmiyor: örneğin, uzmanlar bunun "yerel olarak bağlantılı" olduğundan ve sınırının (ki bu sadece çok hareketli bir eğridir) ikinci boyuta sahip olduğundan şüpheleniyor, ancak bu iddiaların hiçbirinin ne olduğu bilinmiyor, elbette öyle ya da böyle. Bu, matematiğin güzelliğinin ve derinliğinin yalnızca tek bir örneğidir, ancak birçok matematiksel nesnenin aksine, güzellik ve derinlik çok görsel ve herkesin görebileceği şekilde erişilebilirdir.